Table Of Content
NF-serpentine FF contact highly decreased the ohmic resistance level of the cell when compared to the other designs according to the impedance (EIS) measurements. In addition, a correlation was observed between the performance and pressure drop test results. The highest-pressure drop was recorded with NF-serpentine FF (4.225 kPa) whereas the lowest is conventional serpentine FF (0.55 kPa). Traditional serpentine pattern is famous for with high-pressure drop structure. Consecutively, the pressure drop tests proved that the manipulations increased the pressure level of the system directly. If the number of times treatments occur together within a block is equal across the design for all pairs of treatments then we call this a balanced incomplete block design (BIBD).
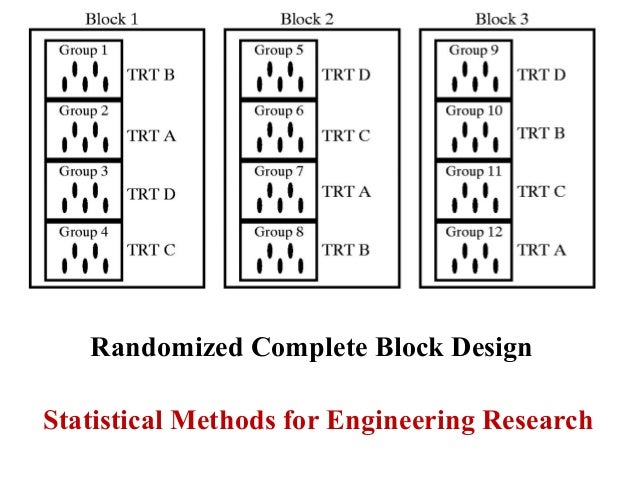
Experimental Design and Blocking
One member of each matched pair must be randomly assigned to the experimental group and the other to the control group. This is a paired design, which is the most simple form of randomized complete block design. The ideal experimental design is the randomized controlled double-blind experiment. We use the usual aov function with a model including the two main effectsblock and variety.
Select appropriate blocking factors
Here are some examples of what your blocking factor might look like. All variables which are not independent variables but could affect the results (DV) of the experiment. To assess the effect of the organization on recall, a researcher randomly assigned student volunteers to two conditions. Instead of a single treatment factor, we can also have a factorial treatmentstructure within every block.
7 - Incomplete Block Designs

If you look at all possible combinations in each row, each treatment pair occurs only one time. Interpretation of the coefficients of the corresponding models, residualanalysis, etc. is done “as usual.” The only difference is that we do not test theblock factor for statistical significance, but for efficiency. I think most of the time it’s just a matter of convention, likely proper to each field. I think that in medical context, in a two factors anova one of the factors is almost always called "treatment" and the other "block". Identify potential factors that are not the primary focus of the study but could introduce variability. In the first example provided above, the sex of the patient would be a nuisance variable.
Dynamic de novo heterochromatin assembly and disassembly at replication forks ensures fork stability - Nature.com
Dynamic de novo heterochromatin assembly and disassembly at replication forks ensures fork stability.
Posted: Thu, 06 Jul 2023 07:00:00 GMT [source]
1.1 Power for completely randomized design
This is usually a constraint given from the experimental situation. And then, the researcher must decide how many blocks are needed to run and how many replicates that provides in order to achieve the precision or the power that you want for the test. Repeated Measures design is an experimental design where the same participants participate in each independent variable condition. This means that each experiment condition includes the same group of participants. By extension, note that the trials for any K-factor randomized block design are simply the cell indices of a k dimensional matrix. In our previous diet pills example, a blocking factor could be the sex of a patient.
Design of Experiments: Blocking
For example, the crops produced in the northern vs the southern part will get exposed to different climate conditions. Controlling these nuisance factors by blocking will reduce the experimental error, thereby increasing the precision of the experiment and many other benefits. In the completely randomized design (CRD), the experiments can only control the random unknown and uncontrolled factors (also known as lucking nuisance factors). However, the RCBD is used to control/handle some systematic and known sources (nuisance factors) of variations if they exist. Note that blocking is a special way to design an experiment, or a special“flavor” of randomization.
Assign treatments to blocks

For example, consider if the drug was a diet pill and the researchers wanted to test the effect of the diet pills on weight loss. The explanatory variable is the diet pill and the response variable is the amount of weight loss. Although the sex of the patient is not the main focus of the experiment—the effect of the drug is—it is possible that the sex of the individual will affect the amount of weight lost.
For a complete block design, we would have each treatment occurring one time within each block, so all entries in this matrix would be 1's. For an incomplete block design, the incidence matrix would be 0's and 1's simply indicating whether or not that treatment occurs in that block. A special case is the so-calledLatin Square design where we have two blockfactors and one treatment factor having \(g\) levels each (yes, all of them!).Hence, this is a very restrictive assumption. In a Latin Square design, eachtreatment (Latin letters) appears exactly once in each row and once ineach column.
Triangular (T) and semicircular (S) obstacles increased the performance significantly. Each manipulation on the traditional serpentine FF affected the power output positively, essentially. The pattern structures of the diagonal semicircle (DS) and diagonal triangular (DT) FFs reduced both water evacuation ability and performance increase rate.
Blocking first, then randomizing ensures that the treatment and control group are balanced with regard to the variables blocked on. If you think a variable could influence the response, you should block on that variable. BlockingWith small samples, it's possible to randomly divide the subjects and still get different groups. In order to address this, researchers “block” subjects into relatively homogeneous groups first and then randomly decide within each block who becomes a part of the control group and who becomes a part of the treatment group.
Gutenberg 14.1 Improves Navigation Block, Adds Experimental Zoomed-Out View - WP Tavern
Gutenberg 14.1 Improves Navigation Block, Adds Experimental Zoomed-Out View.
Posted: Fri, 16 Sep 2022 07:00:00 GMT [source]
The current research proposes to investigate the effects of blocks in various shapes and positions on the net power output by changing the shape of the channels in the flow field (FF). For this reason, semicircular and triangular blocks were machined on the serpentine channels and their short-term performances were compared with the conventional serpentine pattern. In addition to the related new FF designs, performance evaluation was made by using nickel foam placed to fill the inner part of the serpentine FF. First, ultimate operating conditions were optimized with the traditional serpentine FF.
The variable the experimenter manipulates (i.e., changes) is assumed to have a direct effect on the dependent variable. We expect the participants to learn better in “no noise” because of order effects, such as practice. However, a researcher can control for order effects using counterbalancing. In that sense, Latin Square designs are useful building blocksof more complex designs, see for example Kuehl (2000). When I have time to think it through, I'll update this further with the appropriate fancy names for those experiment designs.
In a completely randomized $2\times2$ factorial layout (no blocks), you would completely randomly decide the order in which the breads are baked. For each loaf, you would preheat the oven, open a package of bread dough, and bake it. This would involve running the oven 160 times, once for each loaf of bread. An alternate way of summarizing the design trials would be to use a 4x3 matrix whose 4 rows are the levels of the treatment X1 and whose columns are the 3 levels of the blocking variable X2. The cells in the matrix have indices that match the X1, X2 combinations above.




