Table Of Content
Therefore, it would be very useful to block on gender in order to remove its effect as an alternative explanation of the outcome. And because physical capability differs substantially between males and females, the authors decided to block on gender. So in both experiments we need to do six mass spectrometry runs. We can create a (random) Latin Square design in R for example with thefunction design.lsd of the package agricolae (de Mendiburu 2020). Connect and share knowledge within a single location that is structured and easy to search.
Book traversal links for 4.7 - Incomplete Block Designs
For example, if the study contains the place as a blocking factor, the results could be generalized for the places. A fertilizer producer can only claim that it is effective regardless of the climate conditions when it is tested in various climate conditions. In this case, you would run the oven 40 times, which might make data collection faster.
7 - Incomplete Block Designs
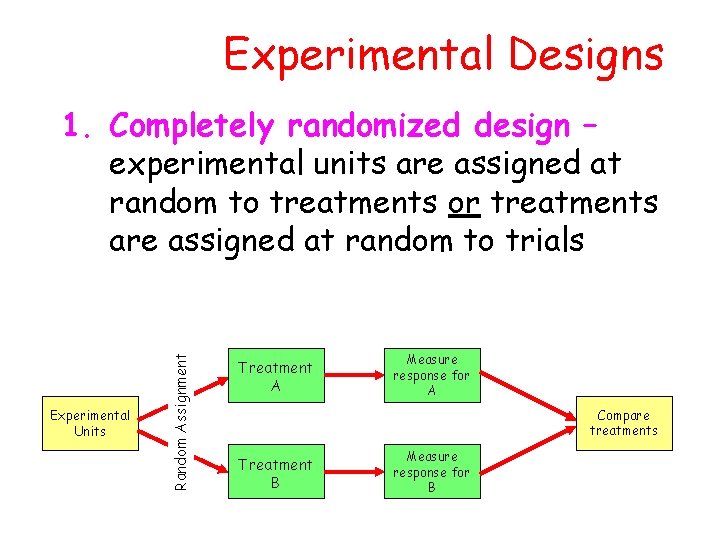
When we can utilize these ideal designs, which have nice simple structure, the analysis is still very simple, and the designs are quite efficient in terms of power and reducing the error variation. A randomized block design is a type of experiment where participants who share certain characteristics are grouped together to form blocks, and then the treatment (or intervention) gets randomly assigned within each block. To address nuisance variables, researchers can employ different methods such as blocking or randomization.
Video 2: Blocking Examples
Fire behavior of hemp blocks: A biomass-based construction material - ScienceDirect.com
Fire behavior of hemp blocks: A biomass-based construction material.
Posted: Fri, 01 Dec 2023 08:00:00 GMT [source]
Blocking is most commonly used when you have at least one nuisance variable. A nuisance variable is an extraneous variable that is known to affect your outcome variable that you cannot otherwise control for in your experiment design. If nuisance variables are not evenly balanced across your treatment groups then it can be difficult to determine whether a difference in the outcome variable across treatment groups is due to the treatment or the nuisance variable. The objective of the randomized block design is to form groups where participants are similar, and therefore can be compared with each other. The term experimental design refers to a plan for assigning experimental units to treatment conditions. Randomly allocating participants to independent variable conditions means that all participants should have an equal chance of taking part in each condition.
What is Blocking?
Then, the performance outputs of the proposed FF designs were compared under the same conditions assigned in the previous section. The single-cell performance tests yielded that the highest power density was ensured with nickel foam (NF)-serpentine FF with 0.267 W/cm2. This increment corresponds to a 38 % enhancement in the power output when compared to the classical serpentine-type FF.
Identify nuisance variables
For each experiment, identify (1) which experimental design was used; and (2) why the researcher might have used that design. Here are the main steps you need to take in order to implement blocking in your experimental design. Imagine an extreme scenario where all of the athletes that are running on turf fields get allocated into one group and all of the athletes that are running on grass fields are allocated into the other group. In this case it would be near impossible to separate the impact that the type of cleats has on the run times from the impact that the type of field has. Note that the least squares means for treatments when using PROC Mixed, correspond to the combined intra- and inter-block estimates of the treatment effects. Since the first three columns contain some pairs more than once, let's try columns 1, 2, and now we need a third...how about the fourth column.
We could put individuals into one of two blocks (male or female). And within each of the two blocks, we can randomly assign the patients to either the diet pill (treatment) or placebo pill (control). By blocking on sex, this source of variability is controlled, therefore, leading to greater interpretation of how the diet pills affect weight loss. Experimental design refers to how participants are allocated to different groups in an experiment. Types of design include repeated measures, independent groups, and matched pairs designs. Note, that the power is indeed much larger for the randomized complete block design.
What is blocking in experimental design?
Each oven run would have four loaves, but not necessarily two of each dough type. (The exact proportion would be chosen randomly.) You would have 5 oven runs for each temperature; this could help you to account for variability among same-temperature oven runs. At a high level, blocking is used when you are designing a randomized experiment to determine how one or more treatments affect a given outcome.
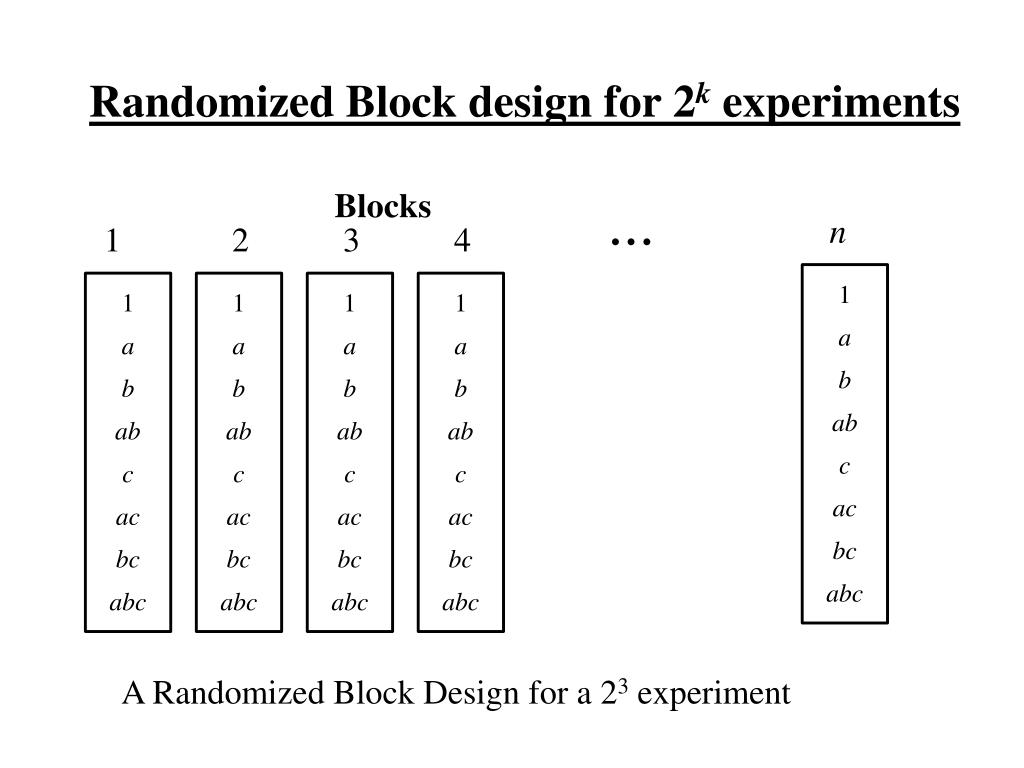
It is good practice to write the block factor first; incase of unbalanced data, we would get the effect of variety adjusted for blockin the sequential type I output of summary, see Section 4.2.5and also Chapter 8. In Design of Experiments, blocking involves recognizing uncontrolled factors in an experiment–for example, gender and age in a medical study–and ensuring as wide a spread as possible across these nuisance factors. Let’s take participant gender in a simple 3-factor experiment as an example. The final step in the blocking process is allocating your observations into different treatment groups. All you have to do is go through your blocks one by one and randomly assign observations from each block to treatment groups in a way such that each treatment group gets a similar number of observations from each block. The first step of implementing blocking is deciding what variables you need to balance across your treatment groups.
Suppose engineers at a semiconductor manufacturing facility want to test whether different wafer implant material dosages have a significant effect on resistivity measurements after a diffusion process taking place in a furnace. They have four different dosages they want to try and enough experimental wafers from the same lot to run three wafers at each of the dosages. As an example, imagine you were running a study to test two different brands of soccer cleats to determine whether soccer players run faster in one type of cleats or the other. Further, imagine that some of the soccer players you are testing your cleats on only have grass fields available to them and others only have artificial grass or turf fields available to them. Now, say you have reason to believe that athletes tend to run 10% faster on turf fields than grass fields. Switch them around...now first fit treatments and then the blocks.
Randomly dividing the subjects into the 2 groups is the most likely to make the treatment and control groups as alike as possible because it eliminates human bias. Not only differences that the researcher has identified as relevant, but on all characteristics, including the hidden ones that the researcher might not realize are important. The design is balanced having the effect that our usual estimators andsums of squares are “working.” In R, we would use the model formulay ~ Block1 + Block2 + Treat.
His work in developing analysis of variance (ANOVA) set the groundwork for grouping experimental units to control for extraneous variables. A randomized block design is an experimental design where the experimental units are in groups called blocks. The treatments are randomly allocated to the experimental units inside each block.
The single design we looked at so far is the completely randomized design (CRD) where we only have a single factor. In the CRD setting we simply randomly assign the treatments to the available experimental units in our experiment. If we choose one of the RCB Design Structures, Temperature effects are completely randomized at the Run level. Recipe is nested within temperature and has a different error structure than temperature, because each dough appears within each run.
If you have doubts on that your data violates the assumptions you can always simulate data from a model with similar effects as yours but where are distributional assumptions hold and compare the residual plots. In the most basic form, we assume that we do not have replicateswithin a block. This means that we only observe every treatment once in eachblock. The nuisance factor they are concerned with is "furnace run" since it is known that each furnace run differs from the last and impacts many process parameters.
After that, we discuss when you should use blocking in your experimental design. Finally, we walk through the steps that you need to take in order to implement blocking in your own experimental design. When we have missing data, it affects the average of the remaining treatments in a row, i.e., when complete data does not exist for each row - this affects the means. When we have complete data the block effect and the column effects both drop out of the analysis since they are orthogonal. With missing data or IBDs that are not orthogonal, even BIBD where orthogonality does not exist, the analysis requires us to use GLM which codes the data like we did previously.
You can obtain the 'least squares means' from the estimated parameters from the least squares fit of the model. The sequential sums of squares (Seq SS) for block is not the same as the Adj SS. Variable(s) that have affected the results (DV), apart from the IV. A confounding variable could be an extraneous variable that has not been controlled.

No comments:
Post a Comment